September 30, 2024
Jet on a Conveyor Belt

The airplane on the conveyor problem has been around for a while. It keeps popping up in my social media, though. I decided to approach it from a slightly different place, emphasizing the actual performance of the airplane.

The question is poorly-worded. (Physics questions on the Internet are often poorly-worded, to create attention as commenters argue with each other.) No frame of reference is provided for the "speed of the wheels." Nor is the point on the wheel specified. Comic artist and uber-geek Randall Munroe (xkcd) has explored the possibilities. The only scenario which makes physical sense is where the wheel speed is measured from its center of mass relative to Earth, and the conveyor speed is measured in the same way.

The airplane can take off. As it does, the wheels will be spinning at twice their normal rate, which could create problems if engineering specifications are exceeded.

A force diagram for the airplane on the runway is shown below.

It is possible that both drag and lift will be greater than zero at rest, if the airplane is pointed into the wind (as is normal for takeoff). Friction between the wheels and the runway arises from rolling friction and the need to increase the rotational speed of the wheels.

Internet searches yield the following typical data for a 747.

Using this information, we can explore the dynamics of takeoff.

The average acceleration of the airplane during takeoff can be estimated from this video as 1.8 m/s², from zero to 90 m/s in 50 seconds. Nominally, the maximum acceleration would be 2.95 m/s² (=thrust/mass, excluding resistive forces).

The frictional force required to create angular acceleration in the wheels is quite small in relation to the thrust of the engines. Even if this number is doubled by the motion of the conveyor, it is still less than one percent of the engine thrust.

Due to the significant weight of the airplane, the rolling friction of the wheels creates a much greater resistive force, perhaps 7% of the engine thrust.

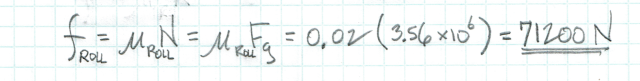
Rolling friction is quite variable depending upon runway surface and total airplane weight. It will be diminished by lift from the wings, which causes normal force to be less than airplane weight.

The original question asks, can the airplane take off? We conclude that the airplane has the net force needed to accelerate to takeoff speed in spite of the conveyor, so long as rolling friction on the conveyor is not excessive. If somehow the conveyor exerted greater resistive forces on the airplane—if its design were more exotic than what we are led to believe—the airplane could of course be prevented from taking off.

September 19, 2024
Process-Based Physics Education

Principles or formulas? Content or process? Effective physics education focuses on all of these, and more.

A meme making the rounds of social media attributes the following quote to Richard Feynman: "Teach principles, not formulas. Understand, don't memorize." If Feynman actually said this, and and I cannot find a definitive source proving he did, it would be out of character for him to be so imprecise. I suspect there was context around this statement the meme is ignoring.

While it's certainly true that memorizing facts and formulas isn't a useful approach to learning physics, ignoring facts and formulas is equally stifling. Formulas are the concise and powerful outcome of our physical understanding of the world, and spoken-word principles don't give us the insights needed to put our knowledge to work.

As an example, let's consider Einstein's theory of special relativity. Its principles include two postulates—that physical laws are identical in all inertial reference frames, and that the speed of light is the same for all observers. Working the postulates into classical kinematics and dynamics yields additional principles, notably mass-energy equivalence and the existence of a spacetime continuum governed by time dilation and length contraction. Reading about the elasticity of space and time predicted the the theory of special relativity has been a source of wonder for physicists and layman alike. But why stop there?

Special relativity formulas rely on the same algebra most of us learned in high school.

With these formulas and a little Googling for values, we can learn why time dilation and length contraction are not readily observable at the typical speeds of terrestrial objects. Or we can determine that the energy produced by a typical nuclear power plant in a day can be obtained from about one gram of matter, the mass of a small paper clip.

A third important consideration, beyond principles and formulas, is the connection between the two: In other words, the answer to the question, "Where do formulas come from?" The time dilation formula above can be derived from the principles of special relativity using simple geometry.

Finally, it's worth getting to the bottom of how experimental inquiry, in this case the Michaelson and Morley experiment which established the invariability of the speed of light, leads to the development of new principles and formulas.

In all of these ways, revealing to students the processes of physics, and expecting them to draw evidence-based conclusions from data, from principles, and from formulas, builds in them the confidence needed to become rational problem solvers in their careers and in their lives. The curricula of the present-day AP Physics courses—their dependence on requiring students to "justify their answer," "explain their reasoning," "determine," and "calculate"—encourage students to engage in the processes of physics. Process-based activities and assessment can be infused into physics courses at all levels.

As "grist for the mill," memorization of principles and content is a good thing, so long as it doesn't end there. Process (laboratory inquiry, derivation, applied reasoning) is the "string" connecting content (principles and formulas) into a web of understanding.