Time and Space | Posts Filtered by Tag

Ever since 1996, when Ingmar Backman did his legendary backside air up in Riksgränsen, I’ve been wondering: how big can a human actually go in a quarter — purely in theory?

Today, approximately 29 years later, I finally chat:ed my way to the answer (feel free to double-check the math and send feedback).

With the right height and transition on the quarterpipe, and a carefully calculated speed that a pair of well-trained thighs can withstand. I’ve come up with this:

I crunched the numbers using the laws of physics and assumed the rider can handle 4 g in the transition. Here are the formulas and calculations:

1. Total g-force in a quarterpipe:

g_total = (v² / (r × g)) + 1

Where:

• `v` = speed in m/s

• `r` = radius of the quarterpipe (in meters)

• `g` = 9.82 m/s² (gravitational acceleration)

2. Maximum speed without exceeding 4 g:

v² = (4 − 1) × r × g = 3 × r × g

3. Converting speed to height (all kinetic energy → height):

h = v² / (2g)

Insert v² from above:

h = (3 × r × g) / (2g) = (3/2) × r = 1.5 × r

So the maximum height above the lip becomes:

h = 1.5 × r

4. Example with a 20-meter radius quarterpipe:

h = 1.5 × 20 = 30 meters (above the lip)

Total height from ground = 20 + 30 = 50 meters

5. Speed required:

v² = 3 × 20 × 9.82 = 589.2

v = √589.2 ≈ 24.26 m/s ≈ 87.4 km/h

```

Conclusion:

If you have a quarterpipe with a 20-meter radius and can handle 4 g in the transition — then, theoretically, you can pull off a 30-meter-high air.

So... what are you all waiting for out there?

Ingmar Backman at the apex of his remarkable jump

Ingmar Backman's backside air, Riksgränsen Sweden, May 1996

My Reaction

My first response built on the assumptions in the OP. Given a landing in a 20-m radius quarter pipe, the maximum g's occur at the bottom of the quarter pipe, where normal force is opposite weight, not at the lip, where normal force is perpendicular to weight. So the calculation shows maximum height from the bottom of 30 m, and maximum height above the lip of 10 m, ignoring friction and air resistance.

If the person center frame is 1.8 m (71") tall, the height of this jump is 1.8•4.6 = 8.3 m above the lip, a good fit for a theoretical maximum of 10 m.

Then I Googled for and watched video of the jump. I realized some of the assumptions in the OP needed revision. The launch speed was limited by the terrain of the lead-in to the quarter pipe, and the ability of the rider to max out on speed during the lead-in. The landing zone could definitely not be modeled as a circular arc. Better to model it as a steep inclined plane, with landing impact on the slope. And finally, the parabolic trajectory of the jump is too large to ignore. The take-off ramp was not vertical at the lip.

To achieve a jump height of 8.3 m, the vertical component of Ingmar's speed at the lip would have to be 13 m/s, or 29 mph. With the angle of the ramp taken into account, the resultant speed would be no more than 15 m/s, or 34 mph. The long, uphill lead-in to the ramp scrubbed off a lot of speed.

Here is a good analysis of g's during snowboard landings, and the impact of a sloped landing zone. While in theory snowboarders might experience 14 g's at landing, the actual number is usually quite a bit less. What matters is the impact velocity perpendicular to the slope, and the time it takes for that velocity to zero out.

Frame-by-frame analysis of the landing shows that Ingmar bends his knees some, but also bends hard over at the waist, allowing his lower body to continue falling, and almost allowing his head to graze the snow. The sequence takes 5 frames or 0.2 seconds.

If the speed at impact is 15 m/s, and the angle between the slope and that velocity is 40 degrees, the component of velocity perpendicular to the slope would be no more than 10 m/s. With a stopping time of at 0.2 seconds, the stopping force would be 5 g's, what a roller coaster rider might experience and close to the 4-g maximum assumed in the OP.

For comparison, a Google search yields some compelling analysis to suggest that g's during carved turns are usually less than 2 g's and more often around 1 g or less. For quick reference, a turn at 15 m/s with a radius of 20 m yields a little over 1 g. But these are sustained g's, and they likely wobble quite a bit around the time-averaged value due to bumps and corrections to form.

Estimating the height of the jump

A still frame showing Ingmar's landing posture

Conclusion

Ultimately, the limitation on height of a snowboard jump is speed and angle of approach going into the jump, and the ability of the human body to absorb the forces needed to land. All in all, what a fascinating opportunity to explore the physics of snowboarding.

Share this:

Link: https://shelterphysics.com/blog/Quarter-Pipe-Heights-a1/

September 30, 2024
Jet on a Conveyor Belt

The airplane on the conveyor problem has been around for a while. It keeps popping up in my social media, though. I decided to approach it from a slightly different place, emphasizing the actual performance of the airplane.

The question is poorly-worded. (Physics questions on the Internet are often poorly-worded, to create attention as commenters argue with each other.) No frame of reference is provided for the "speed of the wheels." Nor is the point on the wheel specified. Comic artist and uber-geek Randall Munroe (xkcd) has explored the possibilities. The only scenario which makes physical sense is where the wheel speed is measured from its center of mass relative to Earth, and the conveyor speed is measured in the same way.

Spoiler

The airplane can take off. As it does, the wheels will be spinning at twice their normal rate, which could create problems if engineering specifications are exceeded.

Knowns

A force diagram for the airplane on the runway is shown below.

It is possible that both drag and lift will be greater than zero at rest, if the airplane is pointed into the wind (as is normal for takeoff). Friction between the wheels and the runway arises from rolling friction and the need to increase the rotational speed of the wheels.

Internet searches yield the following typical data for a 747.

airplane weight = 800 kilopounds = 3.56 x 10⁶ N

airplane mass = 3.63 x 10⁵ kg

airplane thrust = 60 kilopounds per engine(4 engines) = 240 kilopounds = 1.07 x 10⁶ N

number of wheels = 18

wheel radius = 0.62 m

wheel mass = 184 kg

wheel moment of inertia = 46 kg•m²

wheel effective coefficient of rolling friction = 0.02 (on concrete)

Using this information, we can explore the dynamics of takeoff.

Calculations

The average acceleration of the airplane during takeoff can be estimated from this video as 1.8 m/s², from zero to 90 m/s in 50 seconds. Nominally, the maximum acceleration would be 2.95 m/s² (=thrust/mass, excluding resistive forces).

The frictional force required to create angular acceleration in the wheels is quite small in relation to the thrust of the engines. Even if this number is doubled by the motion of the conveyor, it is still less than one percent of the engine thrust.

Due to the significant weight of the airplane, the rolling friction of the wheels creates a much greater resistive force, perhaps 7% of the engine thrust.

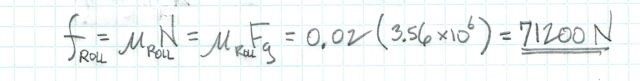
Rolling friction is quite variable depending upon runway surface and total airplane weight. It will be diminished by lift from the wings, which causes normal force to be less than airplane weight.

The original question asks, can the airplane take off? We conclude that the airplane has the net force needed to accelerate to takeoff speed in spite of the conveyor, so long as rolling friction on the conveyor is not excessive. If somehow the conveyor exerted greater resistive forces on the airplane—if its design were more exotic than what we are led to believe—the airplane could of course be prevented from taking off.